Earlier this week, I attended Maths Fest 2025. Maths Fest, run by stand-up mathematician Matt Parker and maths author Rob Eastaway, features some of the best maths speakers in the UK talking about interesting parts of maths, and their favourite bits of maths. The day itself was based at the Royal Institution, the home of groundbreaking science discovery, and it was brilliant. However, one talk stood out to me. This was the Mathematics of Crowd Flow by Professor Aoife Hunt.
Hunt, a simulation modelling specialist and Professor of Crowd Safety and Security Science at the University of Greenwich, opened on the premise that everything is ‘maths in disguise’ and posed the question: “How long would it take to evacuate a venue?” It turns out the answer can be broken down into three elements: site models, flow of people, and human psychology.
Site Models
 An example of a simulation model from crowddynamics.
An example of a simulation model from crowddynamics.
Site models consider the variables of a venue. In the case of an arena this may include stages, different facilities, exits, and the distribution of sections. These work in parallel with each other to determine where people may congregate. Thus, simulations, utilising this information, can predict how attendees will exit the arena. However, more information is needed, this leads onto the concept of ‘flow rate’.
Prof. Hunt described flow rate as the measure of people passing a point in a given time. This will be affected by the width of pathways alongside the density of people. She introduced a few studies showing flow rate against density as a quadratic, giving an optimum number of two people per square metre. In simple terms, this means that even the fastest walkers will slow down significantly. Walking speed of attendees reflects who people are, and what they do. Walking speed is a normal distribution, meaning most people are in the middle. However, this cannot be said for all. Take as example how long it takes to use toilet facilities. Prof. Hunt has actually done a study on this! Interestingly, it is instead a log normal distribution – fascinating!
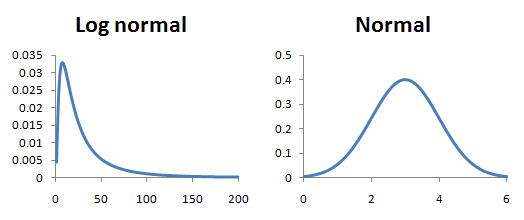 Normal vs a Log normal Distribution
Normal vs a Log normal Distribution
The effect of the pandemic
During the pandemic, an interesting point was raised. Modelling had to include social distancing. This added complexity in the form of a bubble around individuals. This mathematically included circle packing and concluded that a beehive stacking method would be the most efficient way to pack people into a room (given they all stand still!).
A Conclusion
This talk was fascinating to listen to and made me think more about the role mathematics has to play past the engineering design of a structure. Whilst fun, the serious purpose to this is to allow mathematicians to answer these questions to help event organisers and architects to create safe and enjoyable events. Prof. Hunt did a sterling job, giving an engaging presentation to a diverse audience of students and teachers. She concluded by encouraging all of us to be a mathematician in the real world, seeing patterns in nature and solving problems.
 An example of maths in nature with fractals.
An example of maths in nature with fractals.
- MATHS FEST 2025 (2025) maths-fest.com
- LINKEDIN (2025), Professor Aoife Hunt MBE. linkedin.com
- Image by Py Pils on Unsplash.
- Cover image by Anna Dziubinska on Unsplash.
- Crowd Dynamics and Evacuation crowddynamics.aalto.fi